1. Basic considerations
One of the most important questions when working with statistics is “Why are we doing this?” Actually, this should be asked before any work is undertaken. In science, there is typically some underlying research answering this question. Proximate examples for such answers are “To find out if this new drug works better than the established ones” or “To describe the effect of inter-cropping on plant growth” while ultimate answers are “To improve medical treatment” or “To find appropriate cultivation techniques”. It is easy to lose track of these ultimate reasons for conducting a statistical analysis. Losing track of the ultimate answer is a high risk especially for the library-oriented environment, where statistics are often computed on a regular basis. In the worst case, the statistics are complied by an IT department and then given back to the people who initially requested them for interpretation. Factors including staff change, time and the fact that the people interpreting the results were not party to the methods of calculation can lead to misinterpretation or to discarding the results entirely. It is therefore a good idea to keep track of the following procedure:
Figure 1: Statistical Workflow
Furthermore, evaluation of the periodic statistics should be done on a regular base, checking why the statistics were requested in the first place, what matters for these statistics and if the statistics are still required.
2. Understanding stochastic processes
In publications of all kinds, one often finds statements such as “In 2007, there were 361 deadly traffic accidents in Switzerland, this is an increase of 6% compared to 2006” or “Graduate students borrowed 361 items from the library this month, which is an increase of 6% compared to last month’s 340.” Such a statement seems very easy to interpret at first glance. Either the number of loans rises, which is usually considered good [1] , or it falls, right? – Not exactly! Let’s have a closer look at the loans example: Every single user decides, more or less independently of the others, whether to borrow an item or not. The probability of a loan transaction can be influenced by weather, upcoming exams, holidays, opening hours, a cute librarian at the desk and a vast number of other things, but it still is a probability. Let’s assume that all of these influencing factors would not change for two consecutive weeks. By understanding this gedankenexperiment [2] as stochastic process, the weekly loan count would most likely be different even though the environment did not change. In case this puzzles you: Roll a die twice. The pip count will most likely be different, even though the environment did not change at all. This is quite a disturbing fact in connection with the above loan statistic, because an increase or decrease is not as explicit as we would like.
Just to show how meaningless the declaration of just two numbers is, I will briefly work out what kind of statement can be established from such a declaration. The nature of those loans (almost independent, small amount of lots of items are loaned) suggests the use of Poisson distributions. It was explained above that the loan rate is influenced by environmental factors. This results in two hypotheses about the unknown, real rate λ: Either λ does not change during the two consecutive weeks or it did change. We call the first hypothesis the null hypothesis H0 and the second hypothesis the alternate hypothesis HA. Don’t confuse this with a change in the weekly loan count. The loan count can change, but even if it does, this does not necessarily mean that λ has changed. It is, however, possible to construct a confidence interval (CI) [3]. In few words, there is evidence against the H0 if the second loan count is not inside the confidence interval around the first loan count. This test can and should be criticized because it relies on approximations and particularly because λ is set to the first loan count, but it has shaped up as a handy quick-test, especially while reading newspapers or annual reports. The math behind all this is:
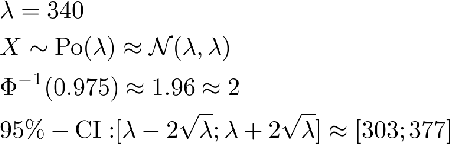
Formula 1: Statistical Formula
Thus the second loan count of 361 is within the confidence interval, hence not providing enough evidence against the H0, so it’s not possible to say that the HAis true, namely that the rates have changed. [4]
3. On communication
In a large library, tasks are usually assigned to different work groups, each may be responsible for end user interaction, fees, acquisition of new items, application maintenance, web design, database interaction and so on. This leads to the generation of statistics by some IT-related work group for one of the other work groups, especially when data retrieval is non-trivial, for instance when the data has to be retrieved directly from an SQL database. This inevitably results in trouble if the workflows are not accurately defined and maintained.
For example, a library may outsource some of its rarely requested items to a depot. This would result in more space for frequently used items, but also in higher transportation costs as well as increased waiting time for the outsourced items. In this scenario there will be a requirement to determine the loan counts of the outsourced items to deduce to determine if an item is loaned often enough to stay at the main library or whether it should be moved to the depot. Somebody not familiar with the workflow would just count the loans on all items. He may not know that the items from the depot, once requested, are loaned on special service accounts to track the transportation process and once they arrive in the main library, moved from the service account to the user’s account when he comes to pick up the item. This means that two loans are registered when an item from the depot is loaned. It is obvious that this has a serious impact on the statistics which are supposed to help with the decision which items should be moved back to the main library. The quintessence here is that people should talk about their workflows and ensure that the staff sticks to them.
Once the modus operandi is clarified, the data can be retrieved with SQL. However, a mechanism is needed to distinguish between the service loans and the “real” loan. In ALEPH 500, a so called event is added to an event table called z35 each time an item is loaned. Luckily, the system distinguishes between simple loans (the “real” loan, event type 50) and transfer loans (the service loan, event type 56). It is crucial that the loans to be counted are restricted to a specific time period of interest. This ensures that the statistics describes the recent state and does not boost items that were interesting years ago, and even more important, that rarely loaned items acquired a long time ago don’t get boosted because the few loans sum up. The resulting SQL looks like this [5]:
select z35_rec_key, z35_item_sequence, count(*) from z35 where z35_sub_library=’E16’ and z35_event_type=50 and z35_event_date between ’20080101’ and ’20081231’ group by z35_rec_key, z35_item_sequence order by 3 ;
When statistics are given away, it is always a good idea to spend some time thinking about how the result can be used best by the requester. In this case, the rec key and the item sequence are probably not going to be very helpful. Ideally, the request process for statistics of any kind should enforce that the requester declares what information should be on the list. In this case, it may be useful to provide title and author of the item [6]:
select z13_author, z13_title, z35_item_sequence, count(*) from z13, z35 where z13_rec_key=z35_rec_key and z35_sub_library=’E16’ and z35_event_type=50 and z35_event_date between ’20080101’ and ’20081231’ group by z13_author, z13_title, z35_item_sequence order by 4 ;
4. Exploring user behavior
Some time ago, we had to investigate the user behavior on our WebOPAC to model a benchmark [7]. To design an appropriate benchmark, three things had to be figured out. First we were interested in how many users were using the system simultaneously at a given time of the day, second it was important to know what functions our users were using and third, we had to know how long they were waiting between the clicks. This is referred to as thinking time in the following and is quite important since it has a huge impact in the resource consumption of the system – a shorter thinking time leads to a higher resource consumption.
4.1 Amount of Web users
The first task was the easiest one, the other two tasks needed slightly more complex actions but could be achieved in similar ways. The number of active users is logged by the Web server service each time a new user appears. This is an excerpt of the log file:
1 Active users : 000000004 2 WWW-F : FIND-C 3 2009-02-05 06:16:20 63 [001] [vrb] [...]
Unfortunately, the relevant line does not include a time-stamp. However, time stamps are present in lines logging other operations. A small awk script was used to collect these time stamps and output the nearest one together with the number of active users:
1 /^2009-02-05 / {
2 d=$1; t=$2
3 }
4 /^Active users :/ {
5 l = d " " t "," $4;
6 if(length(l)==29) print l;
7 }
The condition length(l)==29 was introduced because the logfile held some malformed lines [8] such as
1 Active users : 2009-02-05 08:41:52 11 [...] 084152
Running this small awk script parses the log file such that it can be processed further:
1 $ time awk -f 2 > active.awk < www.log > active.log 3 4 real 0m18.719s 5 user 0m18.677s 6 sys 0m0.036s 7 $ head active.log 8 2009-02-05 06:21:05,000000000 9 2009-02-05 06:24:19,000000000 10 2009-02-05 06:24:25,000000001 11 2009-02-05 06:24:28,000000002 12 2009-02-05 06:24:42,000000003 13 2009-02-05 06:24:49,000000004 14 2009-02-05 06:24:56,000000005 15 2009-02-05 06:25:02,000000006 16 2009-02-05 06:25:02,000000007 17 2009-02-05 06:25:07,000000008
This data can be visualized with a scatter plot for better understanding. Numerous tools can be used for this purpose – the following listing reads the file active.log, parses the timestamps and draws the plot with the open source statistical computing environment R [9]:
1> raw<-read.table("active.log",sep=",")
2> names(raw)<-c("ts","users")
3> attach(raw)
4> POSIX_ts<-as.POSIXct(ts)
5> plot(users~POSIX_ts,pch=20)
4.2 Further Tasks
As written above, information about what functions were used and about the thinking time can be found using similar approaches. The use of WebOPAC-functions such as searching, listing records or renewing loans are logged and can therefore be counted using simple shell scripts using awk or grep. The thinking time was investigated by parsing the apache log file where time stamps both session cookies and IP were logged. First, the lines related to the CGI were extracted to remove the noise of images and additional files not relevant for the result. Then, the time stamps and session ids were extracted and the resulting list was sorted using the session id as primary sort key and the time stamp as secondary sort key with lower priority. The time stamps were parsed with R as shown above and the time difference (Δt) in seconds between two consecutive time stamps of the same session id was computed using a for-loop. Statistical analysis was then done on Δt using R functions such as mean() (arithmetic mean) and sd() (standard deviation) as well as the robust counterparts median() and mad() (median absolute deviation).
5. Conclusions
Albeit much can be done with statistics, it is very important to keep in mind the reason why something is done and to ask if the result is really going to be accurate enough. It is important in the same way to verify that work flows are followed and to be aware that even the raw data can contain errors or be misleading.
Notes
[1] For the other example involving deadly accidents, an increase would be considered bad.
[2] A gedankenexperiment, or thought experiment, according to Wikipedia, “is a proposal for an experiment that would test or illuminate a hypothesis or theory. Given the structure of the proposed experiment, it may or may not be possible to actually perform the experiment.”
[3] Providing a full introduction to Confidence Intervals (CIs) would go beyond the scope of this article. More information on CIs can be found in any introductory book to statistics.
[4] It is very important to realize that it is also not possible to state that is wrong with the above calculation only.
[5] E16 is the code for the depot library, the rec key identifies the title and the item sequence together with the rec key identifies the item.
[6] ALEPH stores title data in a table called z13, hence this request needs an inner join to the z13 table.
[7] The actual benchmark was carried out after the user behavior was reconstructed using JMeter from the Apache Jakarta Project.
[8] Probably the result of several threads just logging into the file without coordination.
[9] R is available at http://www.r-project.org


Gobals, 2011-09-01
Lot of thanks. . For this information