By Brandon Bellanti

Background

I began this project as a capstone study for my graduate program in library and information science. I was interested in a digital humanities project that would bring together what I was learning related to data mining, database design, data analysis, and linked data. I chose music as a topic of interest because I studied it in my undergrad program and am especially interested in music theory and history.

Throughout music history, composers influenced and borrowed from one another, and these relationships are revealed through music analysis and theory. Some relationships were between teachers and pupils, but others were between rival composers or even between composers and patrons. If composers use the same pattern in their works, there is some relationship represented. This overlap could be as elemental as the use of the same scale or as specific as a musical quotation or set of variations.

In the project outlined here, I perform an analytical task – finding recurring patterns across works – that I’ve done many times before, but using a computer to find these patterns rather than finding them manually. I focused only on the most basic matches using intervals alone, but the same method could be expanded to include other facets of musical patterns as well.

Summary

This paper describes an application of computer-aided musicology. Patterns, or sequences of notes, recurring within data extracted from XML-encoded music scores are considered to represent some existing relationship between works and composers. The paper outlines my process of collecting, transforming, analyzing, and visualizing music score data with Python and other tools.

First, I converted MusicXML files to CSV files, which I loaded into a dataframe. I transformed the note pitches into intervals and converted the intervals to strings. I used a regular expression to find recurring sequences of intervals in the outputted strings, and I stored the returned sequences in a SQLite database along with their respective work titles and composers. Finally, I queried the database and used Matplotlib and MuseScore to visualize the patterns. This workflow is outlined in Figure 1.

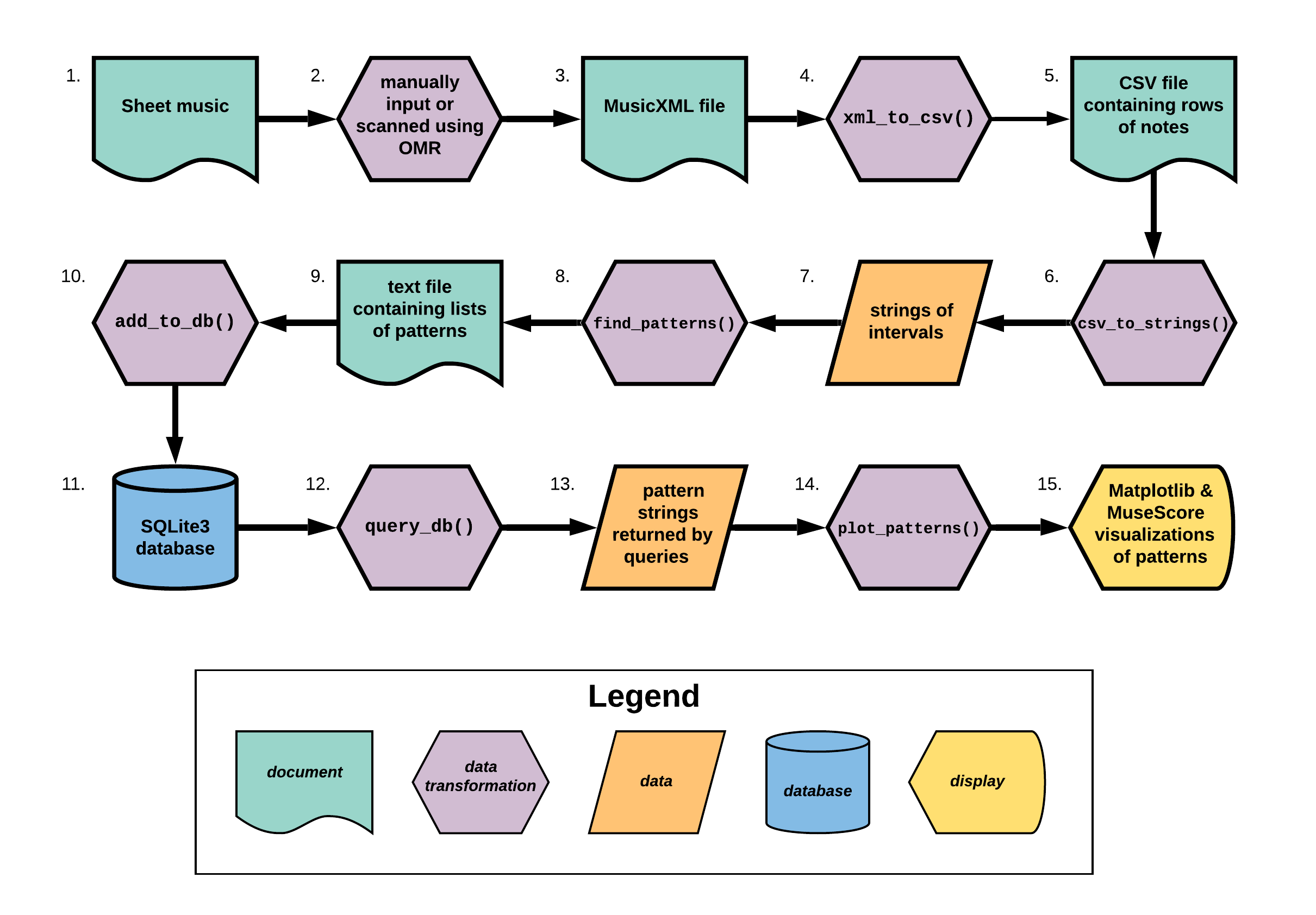
Figure 1. Project workflow for Pythagoras.

Method

Setting up the environment

For this project, I primarily used Python 3 in Jupyter Notebooks. I executed longer-running functions directly through the terminal in Visual Studio Code.

I imported several packages, some standard to Python and others installed with Anaconda. The main ones were lxml, pandas, NumPy, Matplotlib, and SQLite3. Additionally, I used a substitute regex module (Barnett, 2020) and the music21 toolkit (Cuthbert et. al, 2019) for visualizations. The music21 toolkit works in conjunction with MuseScore, an open-source music notation software.

Most of my work was done on a 2015 MacBook Pro 13-inch computer running macOS Mojave; I also used a 2015 MacBook Pro 15-inch computer running macOS Catalina for the more resource intensive processes such as recursively searching for patterns with regular expressions and writing patterns to a database file.

Obtaining XML-encoded music score data

My initial step was finding music score data in a format I could parse with Python. I chose MusicXML because of its wide availability. MusicXML is an XML-based format primarily used for exchanging data between music notation software, meaning I was not limited to working in a specific application.

MusicXML files can be generated by manually inputting scores into a notation software or by scanning sheet music using optical music recognition (OMR). Since MusicXML files are meant to exchange, publish, and archive music scores digitally, it is easy to find files online through collections like Project Gutenberg or the International Music Score Library Project (IMSLP).

The scores I used for this project came from a large collection of files I received upon purchasing a license for Capella Scan, an OMR software. The files I received were in a proprietary format (.cap), so I opened each score file in Capella 8 and exported it as a MusicXML file. I converted a total of 349 files (Figure 1, Steps 1–3), which included digitized piano, orchestral, and choral scores.

Parsing MusicXML files using lxml

After converting the scores to XML files, I used Python’s lxml library to parse the files. The XML elements I used in this project are shown in Figure 2. I also retrieved the values of the id attribute of the part element and the number attribute of the measure element.

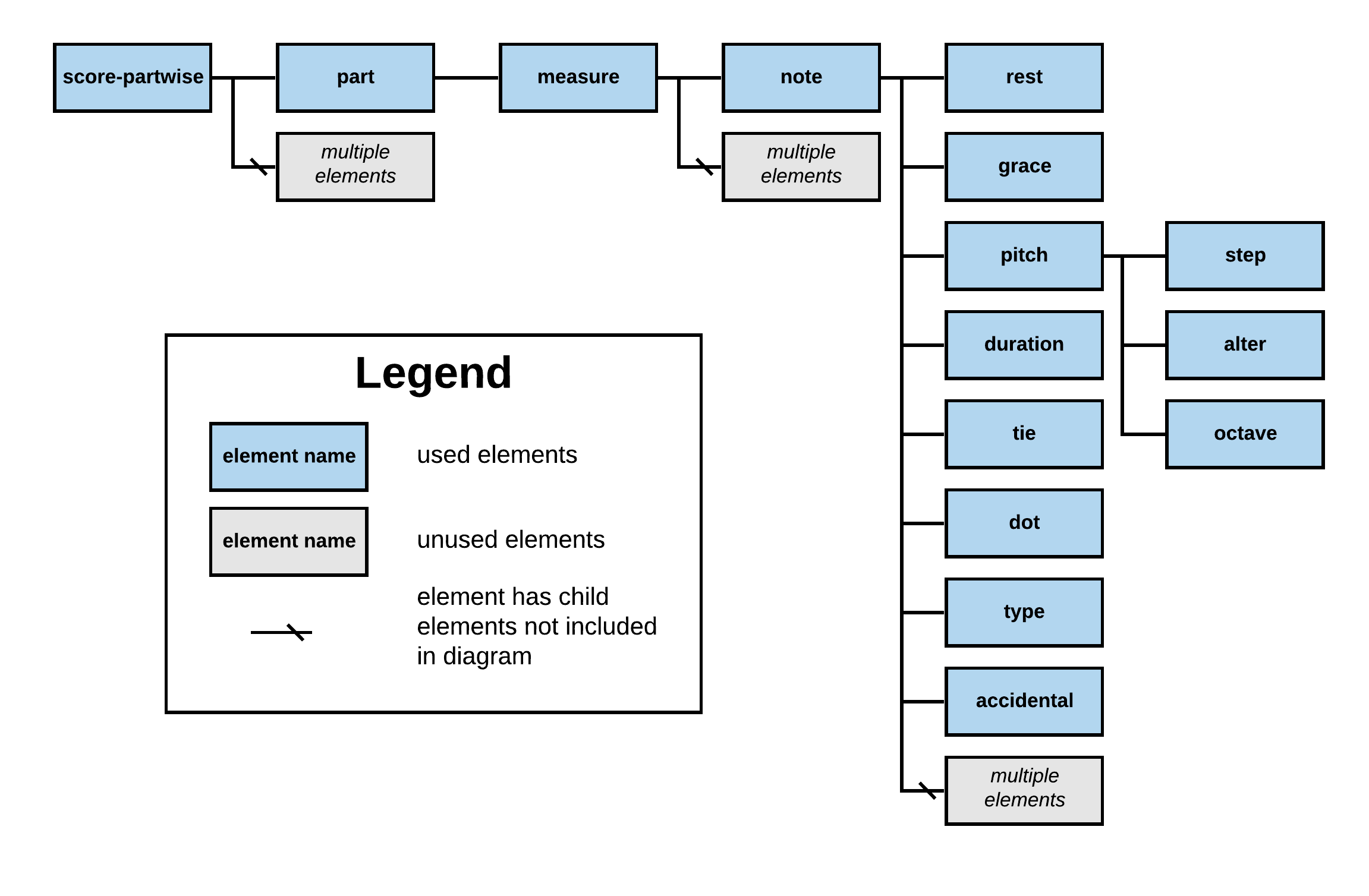
Figure 2. Tree structure of MusicXML files used for this project.

I wrote a function, xml_to_csv() in Figure 3, which iterates over each note element in an XML file (Figure 3a) and writes a line to a corresponding CSV file (Figure 3b) with values for part id, measure number, and note data. Note data includes step, octave, duration, type, and accidentals; it also includes whether the note is a rest, grace note, dotted note, tied note, or cue note. Three of my files had XML-validation errors from the Capella 8 export, but I was able to convert 346 of the 349 XML-encoded scores to CSV files (Figure 1, Steps 3–5).

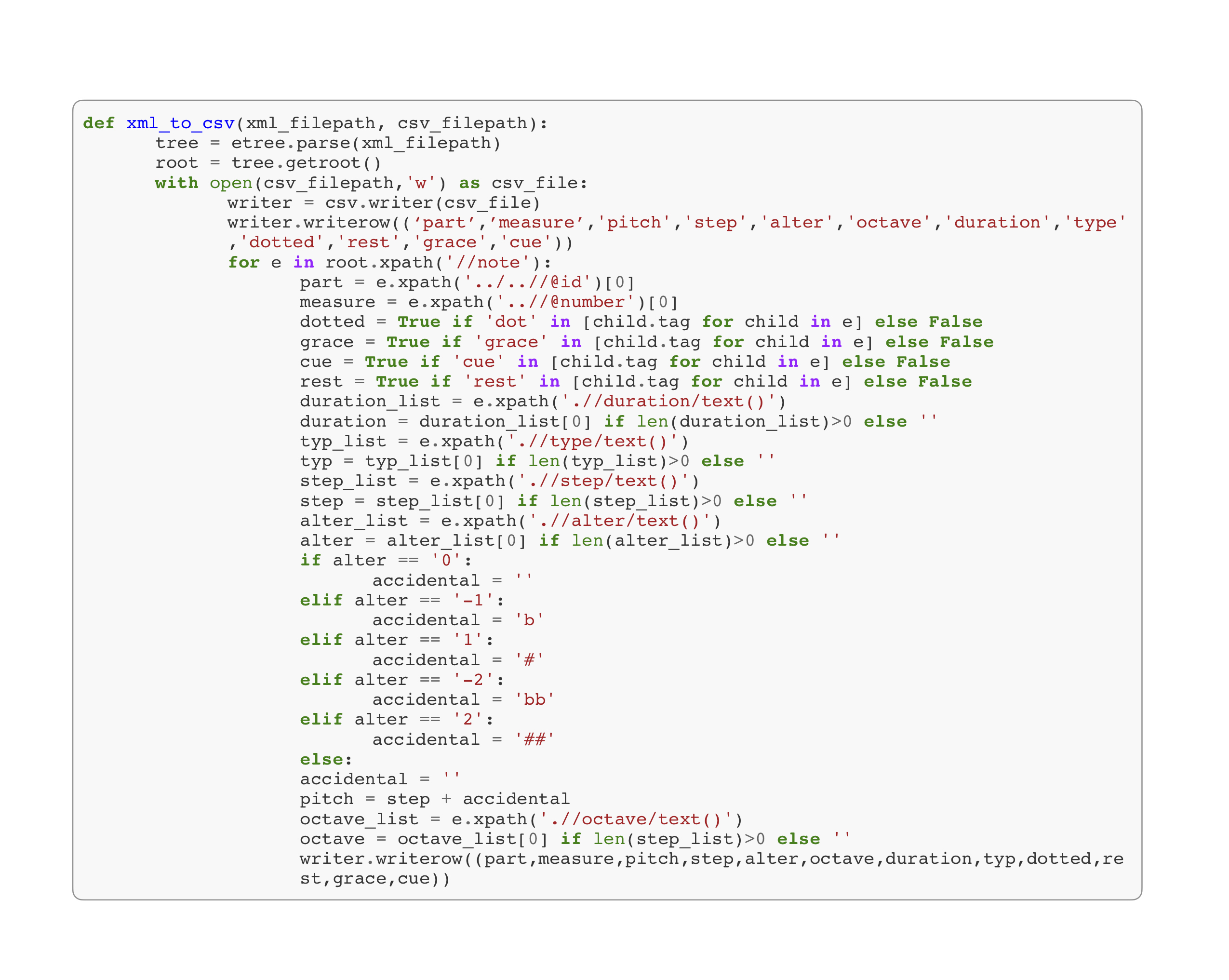
Figure 3. Converting an XML file to a CSV file using xml_to_csv().

Figure 3a. Snippet from an XML file of Mozart’s Twelve Variations on “Ah vous dirai-je, Maman”, K. 265/300e before conversion to CSV

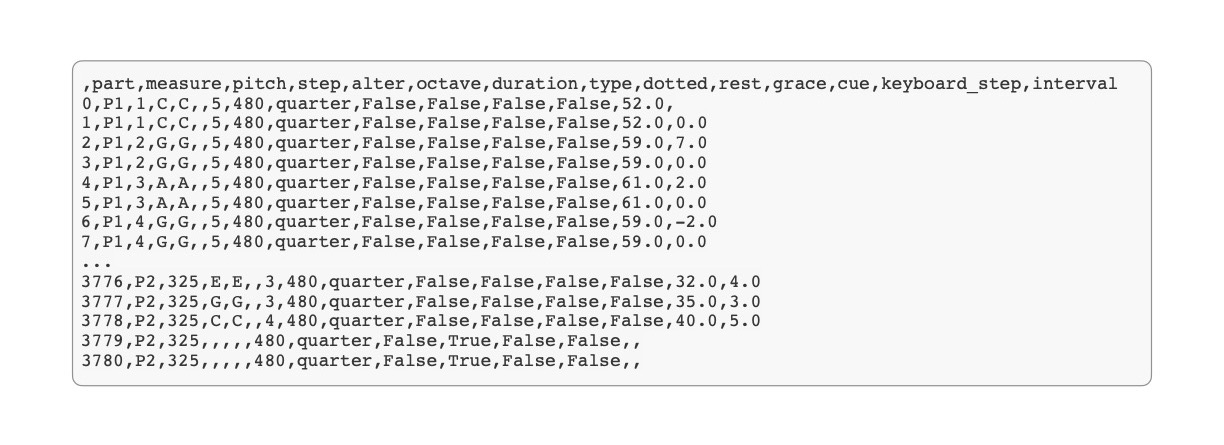
Figure 3b. Snippet from the corresponding CSV file of Mozart’s Twelve Variations on “Ah vous dirai-je, Maman”, K. 265/300e after conversion from XML and interval calculation

Building a dataframe and writing to a string using Pandas

The next step was transforming my data to a format that could be searched for patterns (Figure 1, Steps 5–7). I planned to use regular expressions to find patterns, so I generated a string of pitches for each musical work using the function csv_to_strings() shown in Figure 4.

Figure 4. Reading a file as a dataframe and outputting strings using csv_to_strings().

I loaded each converted CSV file into a dataframe using Pandas’s read_csv() method, each row representing a single note. With all of the pitches in a series (column) in the dataframe, I used the Series.to_string() method to write the pitches to a single, continuous string. I replaced the newline delimiters between the pitches with single dots using string.replace() to make the strings more readable for error checking.

This process worked well, but if I had searched the string at this point, I would only find matching patterns if the pitches were exactly the same. Regex searches could not recognize recurring patterns at lower or higher pitches or in a different key signature. I solved this issue by instead using intervals that showed the relative distance between the pitches. Regardless of the pitch or key signature, the intervals between the steps of recurring patterns would always match.

To calculate intervals, I assigned each note in the dataframe a piano keyboard value based on the pitch and octave. I created a dictionary with each pitch and octave combination as the dictionary key and the piano keyboard number as the value. For example, middle C is C4, which is key 40 on a piano keyboard.

I assigned the notes these values using the Series.apply() method. Once each note had been given a numeric value, I used the Series.diff() method to create a new series of intervals, calculating the difference between consecutive rows of keyboard numbers.

The final step before converting the series to a string was to divide the dataframe by score part. I did this to prevent finding a pattern that occurred only once in each part, as my goal was to find patterns that recurred throughout a work. I iterated through the unique score parts, generated a string of intervals for each part using Series.to_string(), and saved the strings to a dictionary.

Searching for patterns using regular expressions

The core of this project is finding patterns in music score data, and I accomplished that through regular expression (regex) searches (Figure 1, Steps 7–9). Instead of Python’s standard regex library, I used an alternate regex package that could find overlapping matches.
I wrote a regular expression that searches for a pattern of a minimum length that recurs a minimum number of times:

`((?<=\.)[^.]+\.(?:[^.]*\.){%d,}[^.]+(?=\.))(?:.*\1){%d,}`

The expression is built on the following rules:

• The values in the string are delimited with dots.
• The pattern must begin with a non-dot character immediately preceded by a dot; this is implemented through a lookbehind: `(?<=\.)`.
• The pattern must end with a non-dot character immediately followed by a dot; this is implemented through a lookahead: `(?=\.)`.
• The pattern must be at least a certain length; this is implemented by specifying a minimum repetition for a non-capturing group: `(?:[^.]*\.){%d,}`.
• The pattern must recur at least a certain number of times; this is implemented by a non-capturing group that includes a backreference: `(?:.*\1){%d,}`.

The find_patterns() function in Figure 5 takes as its first argument the string dictionary returned from csv_to_string_dict() function. The other arguments are the minimum length of the sequence and the minimum number of occurrences. The argument for minimum length is reduced by two to account for the first and last interval, which are already represented in the regular expression; the minimum occurrences argument is lessened by one to account for the initial occurrence of the pattern.

Figure 5. Searching for patterns in strings with regular expressions using find_patterns().

I saved each returned list of patterns to a unique text file so I could retrieve the patterns without redoing the entire search process. Some of the largest score files were skipped over because the regex searches took too long. I used the func-timeout package to set a five-minute time limit when I ran the find_patterns() function. I did this because a test pattern search through one of the largest files was still unfinished after three hours, though most searches finished well under the time limit. In the end, 313 of the 346 CSV files were successfully converted to strings and searched (Figure 1, Steps 5–9).

Creating a database using SQLite3

After finding the patterns, I created a simple SQLite3 database to store the patterns and their corresponding works (Figure 1, Steps 9–11). The structure of the database is outlined in Figure 6. I created three tables: one for musical works, one for patterns, and one bridge table. There are fields for work and pattern identifiers, the pattern strings, and the work title and composer.

Figure 6. Pythagoras database logical model.

I wrote the function add_to_db() in Figure 7 to read in the text files that held the patterns returned by the find_patterns() function and add data to the three tables. When I had originally converted the Capella files to MusicXML files, I made sure that each file name followed the format: composer_name-work_title.file_extension. Splitting the filename returned values for the composer and work title. Based on the work’s title, I searched for its ID, adding any missing works to the database. I iterated over the patterns in each text file, adding to the database any patterns that hadn’t already been added and retrieving their IDs. I added a row in the bridge table for each work ID and pattern ID combination.

Figure 7. Inserting values into the database using add_to_db()

The database currently holds 346 works from 6 composers containing over 380,000 patterns. I wrote a short function query_db() in Figure 8 which takes an SQL query string and returns an iterable of rows from the query results. The sample query returns the pattern and associated work titles for any patterns that are at least 10 characters long and occur in 5 or more works.

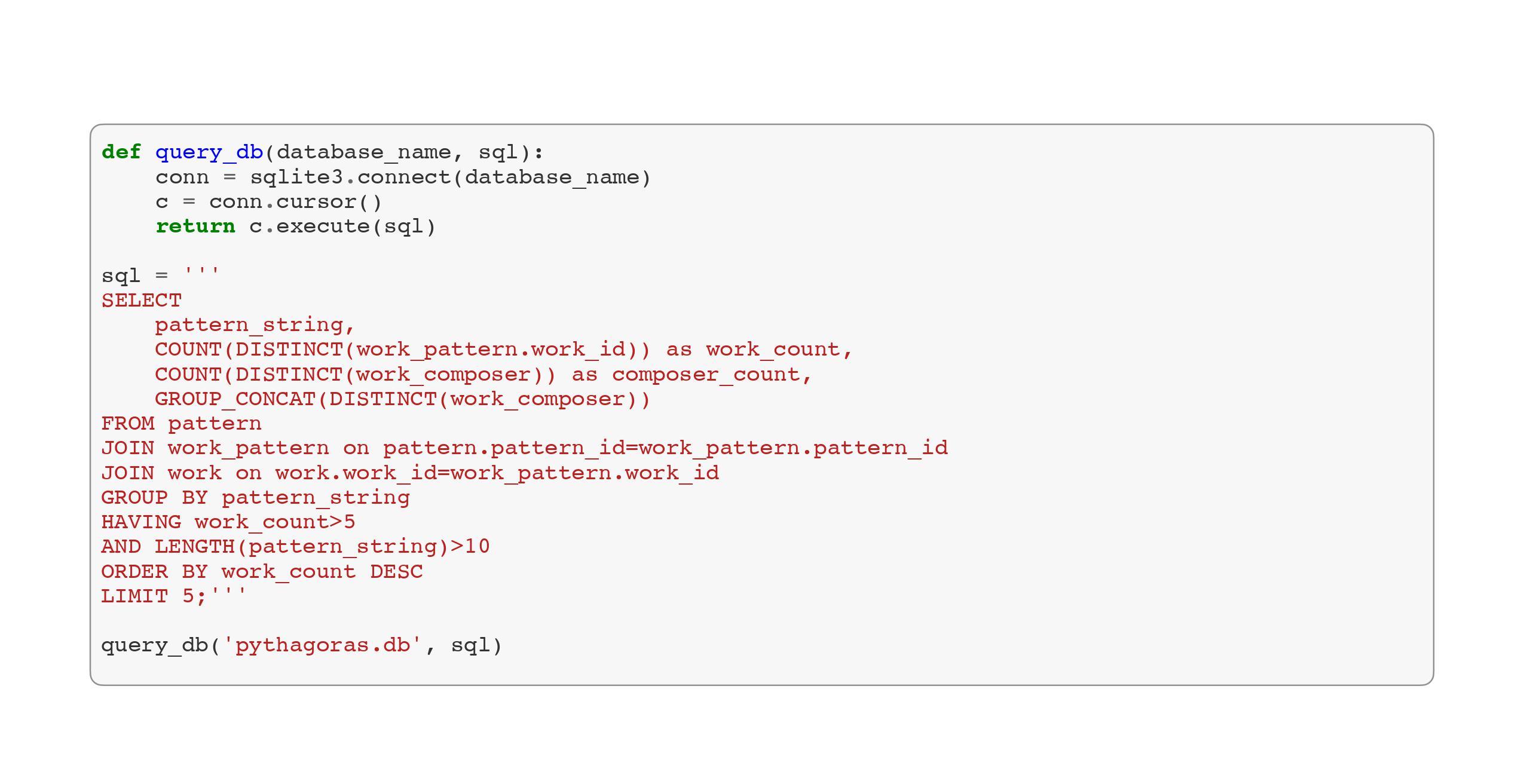
Figure 8. Querying the database using query_db() with a sample query.

Visualizing patterns using Matplotlib and MuseScore

The patterns stored in the database are sequences of intervals; they represent the relative distances between note steps, but not the steps themselves. This was necessary for finding patterns at different pitches or in different key signatures, but it meant that the interval pattern strings must be converted back to sequences of steps in order to visualize the original pattern. I included this conversion in the plot_pattern() function in Figure 9.

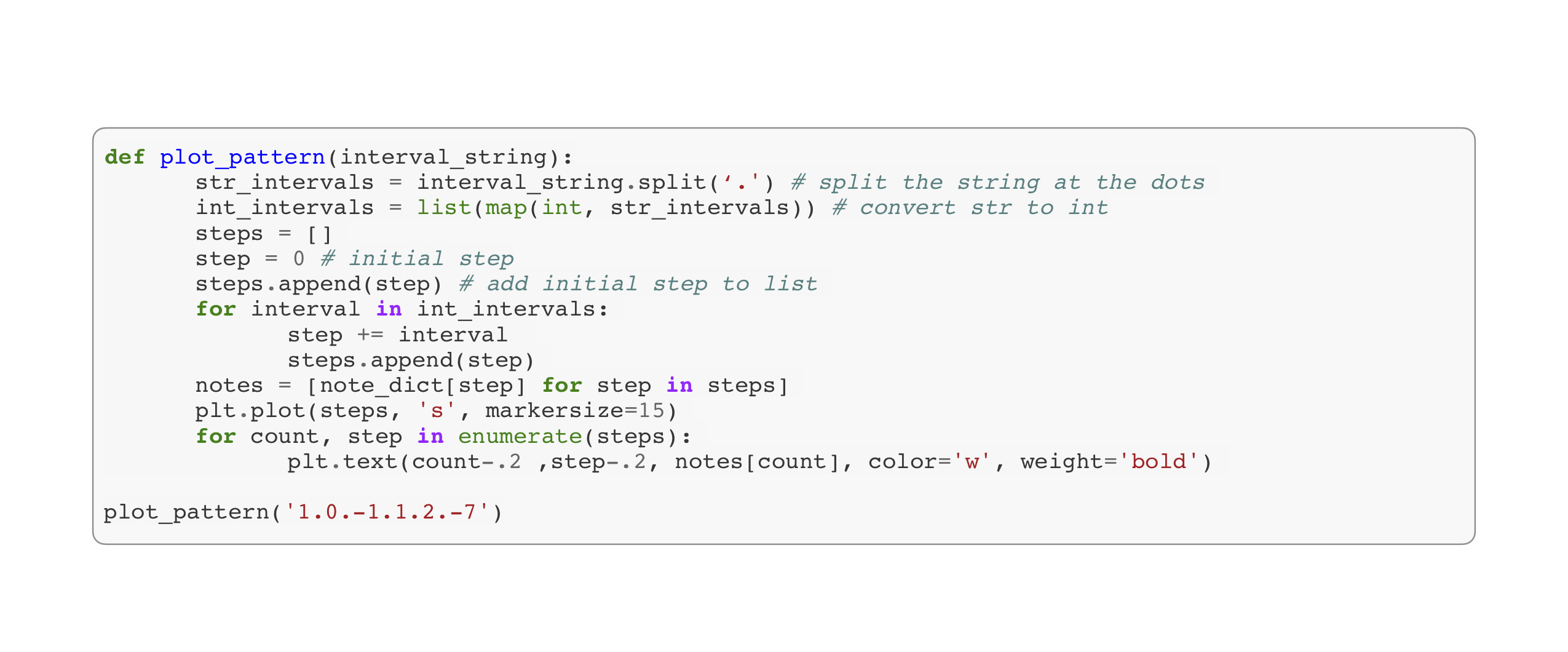
Figure 9. Plotting an interval string with Matplotlib using plot_pattern().

First, I split the interval strings on the dot separators, returning a list of strings. I converted the strings to intervals using the map() method. I created a new list to hold steps and added an initial step of 0, since the first interval represents the relative distance of the second step from the first. For each interval in the interval list, I added its value to the previous step value and appended it to the step list. So, for example, the string ‘1.0.-1.1.2.-7’ was converted the interval list [1,0,-1,1,2,-7] which was used to build the step list [0,1,1,0,1,3,-4] according to the scheme current step + interval = next step:

Initial == 0
0 + 1 == 1
1 + 0 == 1
1 + (-1) == 0
1 + 1 == 1
1 + 2 == 3
3 + (-7) == -4

I plotted the list of steps using Matplotlib, and labeled the steps with provisional pitches based on step 0 representing the pitch C (Figure 10).

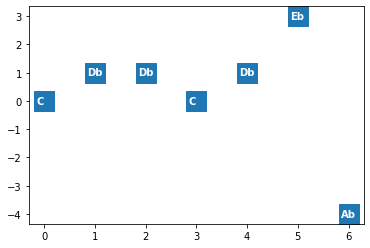
Figure 10. Matplotlib visualization of an interval string, output of code in Figure 9.

I used the music21 toolkit developed by a team at the Massachusetts Institute of Technology to plot the list of steps to a musical staff. Figure 11 shows the output of passing the steps from the example pattern in Figure 9 to Music21’s converter.parse() method. Although this visualization does not necessarily capture the pitches or durations of the original notes, it displays the pattern in a format that is easily recognizable to a musical audience.

Figure 11. MuseScore visualization in Jupyter Notebook using the same pattern as Figure 10.

Challenges

My first major challenge was collecting digitized scores, since optical music recognition software is not yet as functional as I had hoped. I began with the intent of scanning individual scores and exporting them as MusicXML files but found the recognition to be prohibitively inaccurate. Some programs were more accurate than others, but none were effective enough to be considered for this project.

A second challenge was making sure the desired matches were being found by my regular expression searches. I tested simple strings like the pitches for the melody of Twinkle, Twinkle, Little Star before working with longer strings generated by my csv_to_strings() function.

One of the issues I had to solve was making sure both left- and right-anchored matches were returned. The overlapping functionality of the alternate regex library only returned right-anchored matches. For example, a regex search to match four digits in the string ’123456’ would return ’123456’, ’23456’ and ’3456’, but not ’1234’, ’12345’ or ’2345’. To solve this issue, I iterated through the initial list of returned patterns and searched one-by-one through the strings to find any additional matches. Those extra matches were then appended to the list of patterns, as shown in Figure 5.

Another challenge I faced throughout the project was limited computing power. The major steps – converting XML files to CSV files, searching for patterns, and adding patterns to the database – took many hours to run.

Results

This project is still in progress, but my early findings from database queries are promising. I wrote a query for patterns at least 20 characters long and appearing in at least 5 works, and the results included the following:

Pattern: -1.-2.-2.-2.-1.-2.-2
Composers: Beethoven,Schubert,Handel,Mozart
Appears in: 31 works

This result is confirmation that the functions I’ve written are able to successfully parse and convert scores, find and store patterns of intervals, and show at least some relationship between works and composers based on those patterns. This particular sequence, when converted back from intervals to steps, is a descending major scale: 12-11-9-7-5-4-2-0, or C-B-A-G-F-E-D-C in pitches. A next step is to distinguish between commonly used patterns like scales and more unique patterns that would possibly represent a more interesting link between certain works or composers.

Further Work

The work presented in this paper constitutes an introductory approach to the larger goal of using technology to gain new insights into the arts, specifically music. There are several opportunities to expand on the work that I’ve described here.

I will continue to add works and composers to my database. The composers and works included in the project so far represent only a narrow slice of music history. I am particularly interested to see how musical themes have been borrowed across distances in time and place.

Much of the future work has to do with accounting for the complexities of musical patterns. I have, so far, only considered patterns made up of specific intervals, but that is a most basic type of musical pattern. A pattern could be inverted, reversed, shortened, lengthened, or any combination of those variations. It could exchange major intervals for minor intervals, or use completely different intervals altogether and be based on rhythm instead.

There is more information to include about the relationship between the pattern and its respective work. As of now, I can only say whether or not a pattern exists within the notes of the work, but not the number of times the pattern appears or the measure numbers where it began or ended.

Conclusion

Computer analysis can yield insights quickly on a large scale. It is no replacement for trained music theorists, music historians, and musicologists; but it is a useful tool for identifying musical characteristics and relationships that may otherwise go unnoticed. Musical patterns are complex, and their nuance and variation is difficult to account for in the type of searches outlined in this paper. Nevertheless, the results of this initial attempt to show existing relationships using patterns in music score data are promising.

References

Barnett, M. (2020). Regex (Version 2020.4.4). PyPI. https://pypi.org/project/regex/

Cuthbert, M., Ariza, C., Hogue, B., & Oberholtzer, J.W. (2019). Music21: A toolkit for computer-aided musicology (Version 5.7.2). Massachusetts Institute of Technology. http://web.mit.edu/music21/

Savannah, T. (2019). func-timeout (Version 4.3.5). PyPI. https://pypi.org/project/func-timeout/

About the Authors

Brandon Bellanti recently graduated from Simmons University’s Master of Library and Information Science program with a concentration in Information Science & Technology. He can be reached for questions or comments at brandonbellanti@gmail.com.