By M. Bron, M. Proffitt and B. Washburn
Introduction
ArchiveGrid is an aggregation of nearly two million archival material descriptions, including MARC records from WorldCat and finding aids harvested from the web. It is supported by OCLC Research as a corpus for experimentation and testing in text mining, data analysis, and discovery system applications and interfaces. Archival collections held by thousands of libraries, museums, historical societies, and archives are represented in ArchiveGrid. Although roughly 90% of what is in ArchiveGrid are MARC records, as of April 2013 OCLC Research had harvested 124,009 EAD encoded finding aids for inclusion in ArchiveGrid[1]. This small segment of ArchiveGrid is important because EAD has been embraced by the archival community since it’s inception in the 1990s, and is supported by a range of tools designed specifically for archives, such as ArchivesSpace, Archivists’ Toolkit, Archon, CALM, and others.
In creating the ArchiveGrid discovery interface, the project team has wrestled with what we can reasonably do with this corpus. For example, it would be useful to be able to sort by size of collection, however, this would require some level of confidence that the <extent> tag is both widely used and that the content of the tag would lends itself to sorting. Other examples of desired functionality include providing a means in the interface to limit a search to include only items that are in a certain genre (for example, photographs) or to limit a search by date. Again, we would need to have confidence that the metadata we have will actually support these features, and not leave out potentially important collections simply because of the absence of certain tags. Specifically, we will consider how the variability of use of elements in finding aids affects discovery considering five different possible dimensions of a discovery system: search, browse, sort, limit, and display.
As a warning to the reader: this paper delves deeply into EAD elements and attributes and assumes at least a passing knowledge of the encoding standard. For those wishing to learn more about the definitions and structure, we recommend the official EAD website or the less official but highly readable and helpful EADiva site[2].
Related Work
The work that is the most closely related to our research was done by Katherine M. Wisser and Jackie Dean[1]. In 2010 Wisser and Dean solicited EAD files repositories from institutions in order to ”identify encoding behavior.”[3] In total, 108 repositories submitted up to 15 finding aids for the analysis; 1,136 finding aids comprise the entire sample. The formal results of their analysis will be published in the Fall 2013 edition of American Archivist. We are grateful to the authors for sharing their early work with us, and note with interest that in many cases, their analysis of EAD usage is quite similar. However, in some notable cases, the findings from the two samples diverge dramatically (see for example elements in <archdesc> above the <dsc> in Table 9). As noted by Wisser and Dean some of this variation can be attributed to the many different ways in which EAD files can be obtained. Wisser and Dean invited a limited contribution (12-15 finding aids) from a wide variety of repositories, including significant contributions from institutions outside of the US; even though Wisser and Dean carefully articulated that results would be anonymized, there is some chance that the results were somewhat skewed by the process of selecting files for inclusion. By contrast, our data set was assembled by harvesting EAD documents from institutions directly, see below.
Contributing institutions have been motivated to contribute to ArchiveGrid primarily to share information about their collections, not their EAD practices. Additionally, ArchiveGrid is primarily constituted by repositories from the United States, with few institutions from Europe or elsewhere represented in the data set. Either or both of these key differences may account for divergence in findings between our work and that of Wisser and Dean.
The 2010 report, “Implications of MARC Tag Usage on Library Metadata Practices” focused on an analysis of the MARC standard as reflected in World-Cat [5]. Although the emphasis of the the report was, similar to Dean and Wisser, meant to “inform community practice,” a secondary purpose was to draw conclusions about the suitability of MARC data for machine matching and processing, which is similar to our desire to identify functionality (and gaps in functionality) that exist in our current EAD corpus.
OCLC Research regularly harvests EAD documents from contributing institutions to update their representation in the ArchiveGrid index. The update cycle is roughly every six weeks. Institutions are contacted to obtain their permission to harvest and use the data in ArchiveGrid, and to identify the target URLs and rules for selection. For some contributors, the harvesting rules are simple: a directory listing or an HTML page is made available to our crawler, with every link leading to an EAD XML file on the contributor’s server. For other contributors we may make use of a website designed for human visitors, applying custom include and exclude rules to the URLs we find to select only links to EAD documents. Though OAI-PMH repositories and other more specialized harvesting protocols may be available at some contributor sites, we have seen little interest among contributors in their use, and currently we are using only standard HTTP GET requests for all the many hundreds of EAD document providers. Maintaining the EAD harvesting operation continues to be a significant component of the ArchiveGrid support costs covered by OCLC Research.
Methods
Defining Thresholds
It is difficult to predefine thresholds for the level of usage of an element at which it becomes more or less useful for discovery. Is an element that is used 95% of the time still useful but one that is used 94% not? In this paper we consider the thresholds resulting from working with our sample of documents. We will use the terminology documents and finding aids interchangeably throughout the paper.
As an indicator for usage of an element we use the percentage of documents that contain the element at least once (% uniq). The nested nature of finding aids, however, influences the usage of elements as the absence of a parent element reduces the possibility of the occurrence of child elements. As an alternative indicator for usage we use the percentage of documents that contain an element in the sample of documents that contain the element’s parent element (% uniq in C).
Figure 1 shows how often the percentage of usage of an element falls into certain intervals. Note that we use relative usage (% uniq in C) here.
The distribution of element usage could be roughly divided into 4 groups: (i) usage between 0%-50% or low use; (ii) usage between 51%-80% or medium use; (iii) usage between 81%-95% or high use; (iv) usage between 96%-100% or complete use. Although we will use these levels as a reference point in this document, we do so with a recognition that correlating usage with discovery is an artificial construct. In the absence of a more effective approach, we are using these levels as an initial framework for discussion.
The absence of an element does not directly lead to a breakdown in a discovery system. It is more like a gradual decay of the effectiveness of a discovery system. But not all elements are created equally – in current archival discovery systems, we see a range of functionality that is offered, both in terms of search and advanced search options, as well as sorting features, and results display. Within smaller aggregations, we might very well expect tag usage to be considerably more internally consistent than is the case in the ArchiveGrid aggregation. But in the case of ArchiveGrid and similar large aggregations of finding aids, what functionality can be reasonably supported, given the present state of the data? What functionality can we offer with assurance, if we look only at elements that are in the high or complete categories?
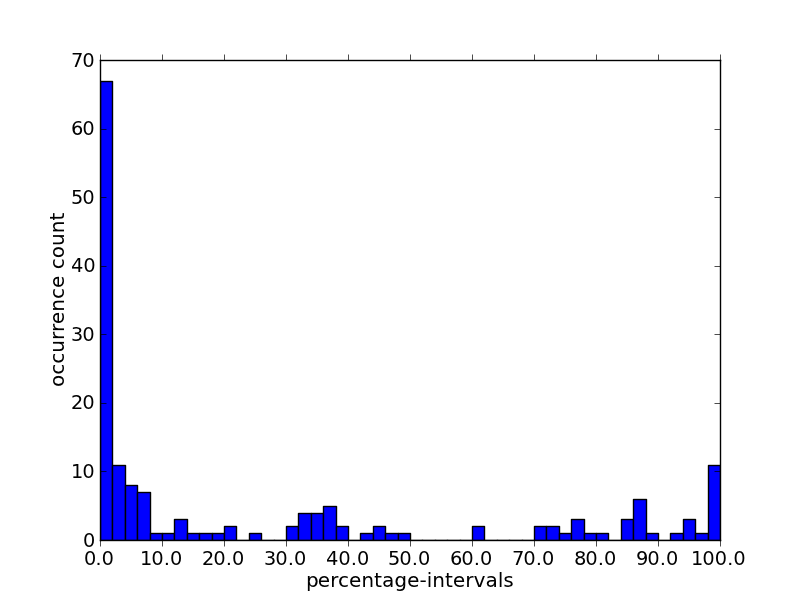
Figure 1: The distribution of percentage of element usage (% uniq in C). Elements are nested and the absence of a parent element influences the occurrence percentage of a child element. For this reason we use the number of element occurrences relative to the occurrences of the parent element (% uniq in C).
Counting Element Occurrences
Finding aids follow the Encoded Archival Description standard, which is a complex XML structure. As an example of the complexity of EAD in implementation, we found more than 26,000 paths in our 129,009 document set. To provide a starting point for obtaining element counts we recreated the many (but not all) tables of element, attribute, and value counts as presented in the report by Wisser et al. [4]. Each table was recreated by performing one or more XPath queries over the corpus of finding aids. In the discussion of our analysis we do not follow the same structure as in Wisser et al. [4] as our focus is on implications of element usage on discovery and presentation. Where appropriate similarities and differences between element usage in our sample of finding aids and those used in Wisser et al. [4] are reported.
In the rest of the paper we use the following notation in our tables: (i) N is the total number of occurrences of an element; (ii) N uniq is the number of documents in which the element occurs at least once; (iii) ![]() is the percentage of documents in our sample of EAD documents (S= 124009) that contain the element at least once; and (iv)
is the percentage of documents in our sample of EAD documents (S= 124009) that contain the element at least once; and (iv) ![]() is the percentage of documents that contain the element in the sample of documents (n=…) that contain a certain element. We will provide the size of each particular sample explicitly. For example, when considering the <eadheader> element that occurs in every document we get
is the percentage of documents that contain the element in the sample of documents (n=…) that contain a certain element. We will provide the size of each particular sample explicitly. For example, when considering the <eadheader> element that occurs in every document we get ![]() , which is the same as
, which is the same as ![]() .
.
We use ![]() to indicate the percentage of documents that contain the element in the sample of documents that contain a certain element as collected by Wisser. In most cases the sample size will be all documents in Wisser’s sample, i.e.,
to indicate the percentage of documents that contain the element in the sample of documents that contain a certain element as collected by Wisser. In most cases the sample size will be all documents in Wisser’s sample, i.e., ![]() . Finally, we use diff to indicate the percentage point difference between the percentage Nuniq and Nuniqk, i.e., between Wisser’s and our sample.
. Finally, we use diff to indicate the percentage point difference between the percentage Nuniq and Nuniqk, i.e., between Wisser’s and our sample.
Dimensions for Analysis
Our analysis considered the following dimensions:
- search: all discovery systems have a keyword search function; many also include the ability to search by a particular field or element: examples include name, date, subject.
- browse: many discovery systems include the ability to browse finding aids: examples include browse by repository, browse by material type.
- results display: once a user has done a search, the results display will return portions of the finding aid to help with further evaluation: examples include title, dates, collection size.
- sort: once a user has done a search, they may have the option to reorder the results. Examples include: order by date, order by title, order by size.
- limit by: once a user has done a search, they may have the option to narrow the results to only include results that meet certain criteria. This may be done through presentation of facets: examples include limit by collections with digital material, limit by repository.
Current discovery interfaces
We reviewed a number of different discovery interfaces for finding aids in order to provide an overview of the type of search, browse, sort, limit, and display options that are generally available. Interfaces included are:
- the Online Archive of California (http://www.oac.cdlib.org/),
- the Northwest Digital Archive (http://nwda.orbiscascade.org/),
- Texas Archival Resources Online (http://www.lib.utexas.edu/taro/index.html),
- Arizona Archives Online (http://www.azarchivesonline.org/xtf/search),
- the Five Colleges Archives and Manuscripts Collection (http://asteria.fivecolleges.edu/index.html),
- the Rocky Mountain Online Archive (http://rmoa.unm.edu/),
- the Harvard Library’s Online Archival Search Information System (http://oasis.lib.harvard.edu/oasis/deliver/home?_collection=oasis).
The interfaces we surveyed are very traditional in the capabilities they support — this is no doubt in part an outcome of the type of functionality that is supported in EAD 2002. In addition to assessing the suitability of the ArchiveGrid corpus for some general archival-specific discovery interfaces, we wanted to cast our net a little wider and speculate on how well EAD may meet the needs of emerging NextGen (or NowGen!) approaches to discovery that may not be represented in our interfaces surveyed, or supported by 2002 era EAD. Emerging discovery apparatus include:
Support for geo-locating archival locations, subjects of collected materials, and other elements, to server map-based search interfaces. Examples of map-based discovery interfaces include:
- HistoryPin (http://www.historypin.com/),
- WhatWasThere (http://www.whatwasthere.com/),
- Historvius (http://www.historvius.com/)
Similarly, we see support for event-based retrieval, using timelines or similar devices, as an area in which discovery systems are evolving. Some examples include:
- SIMILE, example project timeline for Jewish History http://simile.mit.edu/timeline/examples/religions/jewish-history.html,
- Timeline view, Philippine Archives Collection, NARA http://www.archives.gov/research/military/ww2/philippine/timeline.html
- Zagora Archaeological Project http://www.powerhousemuseum.com/zagora/timeline/
Analysis Details
We now take a closer look at which elements might drive each function, how the aggregated data fits this purpose both in terms of meeting our thresholds, and how well the content of key elements are fit for purpose. With each element, we’ve included a note about how they are used in ArchiveGrid and in other discovery systems.
Date
Our analysis shows use of <unitdate> within the high-level <did> as medium (72.64% — see Table 7); This makes <unitdate> values less than reliable for functions such as sort and limit by. Consider, for example, a scenario where a researcher is interested in material from the Second World War. Filtering by a date range between 1939-1945 will result in only those documents being presented that have a <unitdate> assigned in that period and may lead to the researcher missing potentially relevant documents. Alternatively, only those documents could be excluded that have a date outside of the indicated range. However, with a large amount of EADs missing a <unitdate> field this approach defeats the purpose of filtering.
Investing effort to bring this element closer to high or complete may be warranted; however, to support dimensions beyond just display, the content of the field or contents of the “normal” attribute must be easily parseable. When we look at the content of <unitdate>, we find a wide range of descriptive practices, some of which could pose problems for machine parsing to support use in indexing and retrieval.
Another issue involved in using the <unitdate> field is that it can be used in several places, e.g., on its own in the top level <did> or as a subelement of <unittitle>.
Comparing the usage of <unitdate> in our collection of EAD documents and that of Wisser, we find that it is one of the elements where we see the greatest divergence, i.e., Wisser’s sample shows a usage of <unitdate> in the <did> of 97.00%.
In ArchiveGrid, dates are used in:
- search: they are keyword searchable
- display: with the collection title (when available) in brief displays
In other Archival Discovery Systems:
- search
- browse
- sort
- display
Extent
Our analysis shows use of <extent> within the high-level <did> as medium (70.43% — see Table 8); as with <unitdate>, the content of <extent> is quite varied and does not easily facilitate sorting, with values ranging from “miscellaneous artifacts” to “2 ceramic heads.” The syntax of the <extent> element (with attributes for @encodinganalog, @type, and @unit) does not currently lend itself to structuring data in a way that can be used for sorting without clear guidelines, tools to enforce appropriate encoding, and rigor on the part of institutions; retrospectively refitting to be utilized in sorting could be a daunting challenge for many institutions.
Many documents in the ArchiveGrid corpus have multiple <extent> statements, further complicating matters, as the system would need to decide which one to sort, for example. For display, including <extent> statements in order to help aid researchers in evaluating results seems fit to purpose.
In ArchiveGrid, extent is used in:
- search: extent values are keyword searchable
- display: presented in brief displays and separately in the display of individual collection descriptions
In other Archival Discovery Systems:
- sort
- display
Collection Title
Our analysis shows use of <unittitle> in the high-level <did> as complete (99.93% — see Table 7); this would suggest that it is suitable for all uses. However, for sorting and browsing, again, utility depends on the content of the element. If the content of the <unittitle> element is something generic like “Records” or “Papers” (in cases where perhaps the creator has been recorded separately in the origination element), then all functions may be less than ideal, but particularly sorting by title or creating browse lists.
Many interfaces either construct browse lists of collections titles, or allow users to sort results by title, or search within titles. Not surprisingly, we found that the required <filedesc> element in the <eadheader> to be complete. Although our analysis did not include elements below <filedesc>, we can assume that the required <titlestmt> and its required child, <titleproper> will be similarly complete.
The fact that <titlestmt> is fully populated is good news for searching and display; however for sorting and constructing browse lists, we would need to have some assurance that the contents of <titleproper> are fit to purpose. This would be an opportunity for further evaluation, although a quick scan of the contents of <titleproper> encouragingly revealed that 42% of ArchiveGrid finding aids have a @type attribute with the value “filing”, which is rather remarkable as there is no specified list of values for type.
In ArchiveGrid, collection titles are used in:
- search: they are keyword searchable
- display: collection titles appear in brief search results
In other Archival Discovery Systems:
- sort
- browse
- display
Subject
Our analysis shows use of <controlaccess> as medium (72.89% — see Table 9); <controlaccess> is the parent element of both subject as well as other access points (such as <corpname>, <genreform>, <geogname>, and <persname>). Our analysis did not include drilling down to use of <controlaccess> subelements. (Given differences in library and archival practices, we would expect control of form and genre terms to be relatively high, and control of names and subjects to be relatively low.)
In ArchiveGrid, subjects are used in:
- limit by: we show <controlaccess> values for people, groups, places and topics as Result Overview facets for limiting a search result
In other Archival Discovery Systems:
- search
- browse
Material type
Researchers may wish to limit to or seek out material in a specific format, and our survey of discovery systems reveal that some systems support this functionality. Our analysis did not include the children of <controlaccess>, which includes <genreform>.
In ArchiveGrid, material type is used for:
- search: material types in <genreform> are keyword searchable
In other Archival Discovery Systems:
- search
- browse
- limit by
Names (personal or corporate)
Names can be found in multiple places — for the the creator of a collection, is most logically found in <origination>, where both <persname> and <corpname> are child elements. The use of the origination tag is medium (87.78% – see Table 7); our analysis did not include evaluation of the use of <persname> and <corpname> in origination. Otherwise, personal and corporate names as access points may be found in <controlaccess> (see above).
Name elements occur ubiquitously in EAD version 2002, and our analysis did not include a detailed inventory of <persname> and <corpname> in the many places they can occur. A weakness of the distributed nature of names throughout EAD documents is that without detailed annotations and co-references, discovery systems only have a shallow understanding of names and their relationship to the collection and to one another. Discovery systems are not always able to differentiate between names when used in a creator context versus those covered in the description, which may show up as access points.
In ArchiveGrid, names are used for:
- search: names are keyword searchable
- limit by: names for people, groups and places appear in the Result Overview
In other Archival Discovery Systems:
- Used in search
- Used for limiting
Repository
The name of the repository is found in the high-level did in <repository>. Use of this element falls into the promising complete category (99.46%: see Table 7). However, a variety of practice is in play, with the name of the repository being embellished with <subarea> and <address> tags nested within <repository>. To avoid the difficulties in handling these variations across a range of contributing institutions, ArchiveGrid maintains a separate system to manage the form of the institution name for use in the system.
In ArchiveGrid, <repository> is not used as an access point, though ArchiveGrid’s separately administered and controlled form of the repository name is used for search, browse, sort, limit and display.
In other Archival Discovery Systems, used in:
- browse
- limit by
Scope note, biographical note, abstract
Our analysis shows use of <scopecontent> as high (84.41% — see Table 9), while <bioghist> (70.42% — see Table 9) and <abstract> (79.20% — see Table 7) are medium; all three are suitable for search and for display in a results view, although they can be quite lengthy.
For search, its worth noting that the semantics of these elements are different, and may result in unexpected and false “relevance” for matches against descriptions in <bioghist> (about the person) and <scopecontent> and <abstract> (which may be more about the collection).
In ArchiveGrid, these notes are used in:
- search: notes are keyword-searchable
- display: <scopecontent> notes appear (in truncated form if lengthy) in brief search results
In other Archival Discovery Systems, used in:
- search
- display (in snippets or in their entirety)
Collections with digital content
Our analysis did not explore the use of <dao> or <daogrp> elements, which can be used in a variety of places in EAD 2002. Wisser and Dean found that <dao> is used in 7.7% and 9.3% of the documents in their sample, putting both into the low category (see Wisser, Table 26, <dao> elements). However, with growing interest in digitized materials from archival collections, identifying those materials is of increasing importance.
In ArchiveGrid, we provide no mechanism for searching or identifying collections with digital content.
In other Archival Discovery Systems:
- Limiting results to those with digital content
- Flagging collections with digital content
Future Work
In order to make EAD-encoded finding aids more well suited for use in discovery systems, the population of key elements will need to be moved closer to high or (ideally) complete. However, it is not only a matter of populating the elements, but ensuring that the data will reliably power key aspects of discovery systems. This will take concerted effort and tools, both on the part of individual institutions and groups.
In the analysis of “NextGen” discovery services, we noted the use of geolocation-based discovery. Although we would need to do further analysis in <controlaccess> to assess the usage for <geogname> in our document set, the current structure of the <geogname> element does not support geolocation functionality. However, as part of the redesign for EAD3, EAD is becoming more supportive of linked data and linked data structures. This may offer some hope for retrofitting EAD data to be more suited for the task of meeting map-based discovery requirements.
Likewise, the data we have on hand does not suggest good support for event-based discovery, which would draw on well-structured dates, geographic subject terms, and topical subject terms (such as “Battle of Alma” or “Great Depression”). Again, EAD 2002 does not support the sort of encoding that would be necessary to serve event-based discovery, but EAD3 may provide more appropriate structures.
An Optimum Threshold for Discovery?
The picture for archival discovery and EAD is decidedly mixed. On the one hand, we have elements that are in high or even complete use. On the other hand, we have many elements that are necessary for discovery interfaces that are in medium use; and even with elements that are in high or complete use, the contents of those tags are not always fit to purpose. This can be at least partly explained by EAD’s history. In the early days of EAD the focus was largely on moving finding aids from typescript to SGML and XML. Even with much attention given over to the development of institutional and consortial best practice guidelines and requirements, much work was done by brute force and often with little attention given to (or funds allocated for) making the data fit to the purpose of discovery.
Tag analyses such as the work described in this paper can help inform the development and implementation of the EAD schema (indeed the work done by Wisser and Dean was considered in the development of EAD3). But our analysis suggests that the standard has most of the elements and attributes needed to effectively support discovery; what’s missing is agreement on and widespread application of best practices tied to supporting discovery.
So, is the container list half empty? If the archival community continues on its current path then the potential of the EAD format to support researchers or the public in discovery of material will remain underutilized. Minimally, collection descriptions that are below the thresholds for discovery will hinder their discovery efforts and maximally will remain hidden from view. Our paper provides suggestions for the elements where additional effort and investment are warranted to improve their utility for discovery systems. (We recognize that for some institutions, that additional effort may not be feasible or warranted; for their purposes they may find that HTML or PDF collection descriptions suffice.)
Or is the container list half full? Perhaps with emerging evidence about the corpus of EAD, continued discussion of practice, recognition of a need for greater functionality, and shared tools both to create new EAD documents and improve existing encoding, we can look forward to further increasing the effectiveness and efficiency of EAD encoding, and develop a practice of EAD encoding that pushes collection descriptions across the threshold of discovery.
Tables
Table 1: (Wisser Table 1): General statistics for EAD finding aids, using queries: /ead/*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=124009] |
% [(N_uniqK)/n=1136] |
diff |
|
eadheader |
124009 |
124009 |
100.00 |
100.00 |
100.00 |
0.00 |
|
archdesc |
124009 |
124009 |
100.00 |
100.00 |
100.00 |
0.00 |
|
frontmatter |
46115 |
46115 |
37.19 |
37.19 |
24.60 |
12.59 |
|
eadgrp |
0 |
0 |
0.00 |
0.00 |
0.00 |
0.00 |
|
archdescgrp |
0 |
0 |
0.00 |
0.00 |
0.00 |
0.00 |
|
dscgrp |
0 |
0 |
0.00 |
0.00 |
0.00 |
0.00 |
Table 2: (Wisser Table 2): Elements used within eadheader, using query /ead/eadheader/*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=124009] |
% [(N_uniqK)/n=1136] |
diff |
|
eadid |
124445 |
124008 |
100.00 |
100.00 |
100.00 |
-0.00 |
|
filedesc |
124009 |
124009 |
100.00 |
100.00 |
100.00 |
0.00 |
|
profiledesc |
123103 |
123103 |
99.27 |
99.27 |
98.10 |
1.17 |
|
revisiondesc |
42504 |
42501 |
34.27 |
34.27 |
32.70 |
1.57 |
Table 3: (Wisser Table 3) Attributes used with eadheader, using query //eadheader.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=124009] |
% [(N_uniqK)/n=1136] |
diff |
|
countryencoding |
107412 |
107412 |
86.62 |
86.62 |
89.50 |
-2.88 |
|
dateencoding |
107377 |
107377 |
86.59 |
86.59 |
88.20 |
-1.61 |
|
findaidstatus |
42910 |
42910 |
34.60 |
34.60 |
27.80 |
6.80 |
|
langencoding |
117641 |
117641 |
94.86 |
94.86 |
95.00 |
-0.14 |
|
repositoryencoding |
106370 |
106370 |
85.78 |
85.78 |
87.80 |
-2.02 |
|
scriptencoding |
95230 |
95230 |
76.79 |
76.79 |
77.60 |
-0.81 |
Table 4: (Wisser Table 4): Attributes used with eadid, using query //eadid.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=124009] |
% [(N_uniqK)/n=1136] |
diff |
|
countrycode |
108668 |
108667 |
87.63 |
87.63 |
94.30 |
-6.67 |
|
mainagencycode |
105351 |
105350 |
84.95 |
84.95 |
92.60 |
-7.65 |
|
publicid |
45758 |
45758 |
36.90 |
36.90 |
31.10 |
5.80 |
|
url |
38020 |
38020 |
30.66 |
30.66 |
42.30 |
-11.64 |
|
urn |
2312 |
2312 |
1.86 |
1.86 |
3.90 |
-2.04 |
|
identifier |
57260 |
57260 |
46.17 |
46.17 |
49.30 |
-3.13 |
Table 5: (Wisser Table 8): Elements within frontmatter, using query /ead/frontmatter/*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=46115] |
% [(N_uniqK)/n=279] |
diff |
|
titlepage |
45726 |
45726 |
36.87 |
99.16 |
92.80 |
6.36 |
|
div |
190 |
190 |
0.15 |
0.41 |
2.20 |
-1.79 |
Table 6: (Wisser Table 9): Values for @level within archdesc, using query //archdesc/@level.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=124009] |
% [(N_uniqK)/n=1,136] |
diff |
|
collection |
116957 |
116957 |
94.31 |
94.31 |
90.90 |
3.41 |
|
fonds |
135 |
135 |
0.11 |
0.11 |
4.80 |
-4.69 |
|
class |
9 |
9 |
0.01 |
0.01 |
0.30 |
-0.29 |
|
recordgrp |
433 |
433 |
0.35 |
0.35 |
1.40 |
-1.05 |
|
series |
2394 |
2394 |
1.93 |
1.93 |
0.60 |
1.33 |
|
subfonds |
49 |
49 |
0.04 |
0.04 |
0.30 |
-0.26 |
|
subgrp |
526 |
526 |
0.42 |
0.42 |
1.00 |
-0.58 |
|
subseries |
46 |
46 |
0.04 |
0.04 |
0.00 |
0.04 |
|
file |
2446 |
2446 |
1.97 |
1.97 |
0.40 |
1.57 |
|
item |
987 |
987 |
0.80 |
0.80 |
0.30 |
0.50 |
|
otherlevel |
25 |
25 |
0.02 |
0.02 |
0.10 |
-0.08 |
Table 7: (Wisser Table 10): Elements within archdesc/did, using query /ead/archdesc/did/*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=124009] |
% [(N_uniqK)/n=1,136] |
diff |
|
abstract |
102792 |
98218 |
79.20 |
79.20 |
86.60 |
-7.40 |
|
container |
5447 |
3471 |
2.80 |
2.80 |
0.40 |
2.40 |
|
langmaterial |
112938 |
109232 |
88.08 |
88.08 |
89.90 |
-1.82 |
|
materialspec |
41 |
41 |
0.03 |
0.03 |
1.60 |
-1.57 |
|
origination |
113684 |
108853 |
87.78 |
87.78 |
89.00 |
-1.22 |
|
physdesc |
135126 |
122402 |
98.70 |
98.70 |
97.20 |
1.50 |
|
physloc |
53564 |
45620 |
36.79 |
36.79 |
27.80 |
8.99 |
|
repository |
123343 |
123330 |
99.45 |
99.45 |
99.60 |
-0.15 |
|
unitdate |
97247 |
90080 |
72.64 |
72.64 |
97.00 |
-24.36 |
|
unitid |
119911 |
114898 |
92.65 |
92.65 |
90.10 |
2.55 |
|
unittitle |
123959 |
123916 |
99.93 |
99.93 |
100.00 |
-0.07 |
Table 8: (Wisser Table 11): Elements within archdesc/did/physdesc, using query /ead/archdesc/did/physdesc/*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=124009] |
% [(N_uniqK)/n=1,136] |
diff |
|
dimensions |
666 |
576 |
0.46 |
0.46 |
1.80 |
-1.34 |
|
extent |
122613 |
87339 |
70.43 |
70.43 |
76.30 |
-5.87 |
|
physfacet |
2000 |
1520 |
1.23 |
1.23 |
1.70 |
-0.47 |
Table 9: (Wisser Table 12): Elements within archdesc:above the dsc, using query /ead/archdesc/*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=124009] |
% [(N_uniqK)/n=1,136] |
diff |
|
accessrestrict |
55751 |
55579 |
44.82 |
44.82 |
86.20 |
-41.38 |
|
accruals |
694 |
694 |
0.56 |
0.56 |
7.10 |
-6.54 |
|
acqinfo |
40668 |
40451 |
32.62 |
32.62 |
68.00 |
-35.38 |
|
altformavail |
2293 |
2289 |
1.85 |
1.85 |
12.70 |
-10.85 |
|
appraisal |
4613 |
4602 |
3.71 |
3.71 |
4.80 |
-1.09 |
|
arrangement |
40979 |
40627 |
32.76 |
32.76 |
65.50 |
-32.74 |
|
bibliography |
4573 |
4083 |
3.29 |
3.29 |
10.10 |
-6.81 |
|
bioghist |
89103 |
87333 |
70.42 |
70.42 |
87.30 |
-16.88 |
|
controlaccess |
92124 |
90390 |
72.89 |
72.89 |
85.00 |
-12.11 |
|
custodhist |
8375 |
8366 |
6.75 |
6.75 |
14.10 |
-7.35 |
|
descgrp |
67684 |
56446 |
45.52 |
45.52 |
32.00 |
13.52 |
|
fileplan |
50 |
44 |
0.04 |
0.04 |
0.60 |
-0.56 |
|
index |
1231 |
656 |
0.53 |
0.53 |
1.20 |
-0.67 |
|
odd |
9594 |
8145 |
6.57 |
6.57 |
9.70 |
-3.13 |
|
originalsloc |
988 |
973 |
0.78 |
0.78 |
3.40 |
-2.62 |
|
otherfindaid |
6529 |
6271 |
5.06 |
5.06 |
11.90 |
-6.84 |
|
phystech |
900 |
897 |
0.72 |
0.72 |
4.20 |
-3.48 |
|
prefercite |
49015 |
48989 |
39.50 |
39.50 |
85.40 |
-45.90 |
|
processinfo |
27249 |
26623 |
21.47 |
21.47 |
0.00 |
21.47 |
|
relatedmaterial |
23932 |
23676 |
19.09 |
19.09 |
40.30 |
-21.21 |
|
runner |
10822 |
10822 |
8.73 |
8.73 |
1.10 |
7.63 |
|
scopecontent |
105384 |
104670 |
84.41 |
84.41 |
93.40 |
-8.99 |
|
separatedmaterial |
5789 |
5691 |
4.59 |
4.59 |
14.80 |
-10.21 |
|
userestrict |
41365 |
40749 |
32.86 |
32.86 |
68.30 |
-35.44 |
Table 10: Table 13: The inclusion of dsc in finding aids, using query //dsc.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=124009] |
% [(N_uniqK)/n=1,136] |
diff |
|
< dsc > |
98663 |
94473 |
76.18 |
76.18 |
90.30 |
-14.12 |
|
multiple < dsc > s |
98663 |
2075 |
1.67 |
1.67 |
2.40 |
-0.73 |
Table 11: (Wisser Table 14): dsc type attributes, using query //dsc/@type.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=99023] |
% [(N_uniqK)/n=1,105] |
diff |
|
analyticover |
3156 |
3149 |
2.54 |
3.18 |
5.10 |
-1.92 |
|
combined |
49205 |
49184 |
39.66 |
49.67 |
66.50 |
-16.83 |
|
in-depth |
36433 |
35876 |
28.93 |
36.23 |
16.70 |
19.53 |
|
othertype |
1725 |
1572 |
1.27 |
1.59 |
3.50 |
-1.91 |
Table 12: (Wisser Table 15): c-c12 tags, using query //c | //c01 | //c02 | //c03 | //c04 | //c05 | //c06 | //c07 | //c08 | //c09 | //c10 | //c11 | //c12.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=96548] |
% [(N_uniqK)/n=1,053] |
diff |
|
c |
4745698 |
14440 |
11.64 |
14.96 |
11.10 |
3.86 |
|
c01 |
1650659 |
78600 |
63.38 |
81.41 |
88.00 |
-6.59 |
|
c02 |
7432993 |
59217 |
47.75 |
61.33 |
72.50 |
-11.17 |
|
c03 |
6625963 |
29136 |
23.50 |
30.18 |
41.80 |
-11.62 |
|
c04 |
2927180 |
12819 |
10.34 |
13.28 |
20.60 |
-7.32 |
|
c05 |
1312217 |
5587 |
4.51 |
5.79 |
10.70 |
-4.91 |
|
c06 |
598647 |
2266 |
1.83 |
2.35 |
4.60 |
-2.25 |
|
c07 |
261648 |
922 |
0.74 |
0.95 |
2.00 |
-1.05 |
|
c08 |
90401 |
331 |
0.27 |
0.34 |
0.70 |
-0.36 |
|
c09 |
21514 |
110 |
0.09 |
0.11 |
0.30 |
-0.19 |
|
c10 |
3578 |
36 |
0.03 |
0.04 |
0.10 |
-0.06 |
|
c11 |
823 |
7 |
0.01 |
0.01 |
0.00 |
0.01 |
|
c12 |
96 |
2 |
0.00 |
0.00 |
0.00 |
0.00 |
Table 13: (Wisser Table 16): Values for level attribute on c, c/@level, using query //c/@level | //c01/@level | //c02/@level | //c03/@level | //c04/@level | //c05/@level | //c06/@level | //c07/@level | //c08/@level | //c09/@level | //c10/@level | //c11/@level | //c12/@level.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=96548] |
% [(N_uniqK)/n=1,053] |
diff |
|
collection |
13489 |
4782 |
3.86 |
4.95 |
2.10 |
2.85 |
|
fonds |
418 |
95 |
0.08 |
0.10 |
0.70 |
-0.60 |
|
class |
63134 |
2113 |
1.70 |
2.19 |
1.20 |
0.99 |
|
recordgrp |
1535 |
193 |
0.16 |
0.20 |
0.70 |
-0.50 |
|
series |
398727 |
58480 |
47.16 |
60.57 |
77.70 |
-17.13 |
|
subfonds |
3210 |
637 |
0.51 |
0.66 |
1.70 |
-1.04 |
|
subgrp |
5573 |
430 |
0.35 |
0.45 |
3.10 |
-2.65 |
|
subseries |
466366 |
16974 |
13.69 |
17.58 |
35.30 |
-17.72 |
|
file |
11419524 |
36262 |
29.24 |
37.56 |
56.90 |
-19.34 |
|
item |
3480272 |
20415 |
16.46 |
21.14 |
24.20 |
-3.06 |
|
otherlevel |
368942 |
6225 |
5.02 |
6.45 |
9.10 |
-2.65 |
Table 14: (Wisser Table 17): c-c12/did elements, using query //c/did/* | //c01/did/* | //c02/did/* | //c03/did/* | //c04/did/* | //c05/did/* | //c06/did/* | //c07/did/* | //c08/did/* | //c09/did/* | //c10/did/* | //c11/did/* | //c12/did/*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=96548] |
% [(N_uniqK)/n=1,053] |
diff |
|
abstract |
1421043 |
3850 |
3.10 |
3.99 |
2.50 |
1.49 |
|
container |
24951558 |
72377 |
58.36 |
74.96 |
82.50 |
-7.54 |
|
langmaterial |
46798 |
1127 |
0.91 |
1.17 |
6.10 |
-4.93 |
|
materialspec |
22870 |
106 |
0.09 |
0.11 |
1.30 |
-1.19 |
|
origination |
1308346 |
4090 |
3.30 |
4.24 |
8.10 |
-3.86 |
|
physdesc |
3967094 |
37749 |
30.44 |
39.10 |
54.40 |
-15.30 |
|
physloc |
1343791 |
5978 |
4.82 |
6.19 |
5.80 |
0.39 |
|
repository |
34923 |
29 |
0.02 |
0.03 |
0.30 |
-0.27 |
|
unitdate |
9613593 |
41894 |
33.78 |
43.39 |
90.60 |
-47.21 |
|
unitid |
7167784 |
31035 |
25.03 |
32.14 |
46.20 |
-14.06 |
|
unittitle |
25228059 |
92888 |
74.90 |
96.21 |
98.90 |
-2.69 |
Table 15: (Wisser Table 18): c-c12/did/physcdesc elements, using query //c/did/physdesc/* | //c01/did/physdesc/* | //c02/did/physdesc/* | //c03/did/physdesc/* | //c04/did/physdesc/* | //c05/did/physdesc/* | //c06/did/physdesc/* | //c07/did/physdesc/* | //c08/did/physdesc/* | //c09/did/physdesc/* | //c10/did/physdesc/* | //c11/did/physdesc/* | //c12/did/physdesc/*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=96548] |
% [(N_uniqK)/n=1,053] |
diff |
|
dimensions |
144079 |
1378 |
1.11 |
1.43 |
5.20 |
-3.77 |
|
extent |
2401903 |
24495 |
19.75 |
25.37 |
36.60 |
-11.23 |
|
physfacet |
164430 |
613 |
0.49 |
0.63 |
6.80 |
-6.17 |
Table 16: (Wisser Table 19): other elements found in c-c12, using query //c/* | //c01/* | //c02/* | //c03/* | //c04/* | //c05/* | //c06/* | //c07/* | //c08/* | //c09/* | //c10/* | //c11/* | //c12/*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=96548] |
% [(N_uniqK)/n=1,053] |
diff |
|
accessrestrict |
600069 |
4844 |
3.91 |
5.02 |
10.70 |
-5.68 |
|
accruals |
12 |
11 |
0.01 |
0.01 |
0.00 |
0.01 |
|
acqinfo |
68066 |
1477 |
1.19 |
1.53 |
4.50 |
-2.97 |
|
altformavail |
252282 |
766 |
0.62 |
0.79 |
2.70 |
-1.91 |
|
appraisal |
48 |
30 |
0.02 |
0.03 |
0.70 |
-0.67 |
|
arrangement |
31945 |
5746 |
4.63 |
5.95 |
19.00 |
-13.05 |
|
bibliography |
2067 |
48 |
0.04 |
0.05 |
1.50 |
-1.45 |
|
bioghist |
12511 |
1132 |
0.91 |
1.17 |
4.60 |
-3.43 |
|
controlaccess |
243134 |
2149 |
1.73 |
2.23 |
5.10 |
-2.87 |
|
custodhist |
26224 |
181 |
0.15 |
0.19 |
2.20 |
-2.01 |
|
descgrp |
2703 |
31 |
0.02 |
0.03 |
1.80 |
-1.77 |
|
index |
386148 |
835 |
0.67 |
0.86 |
0.70 |
0.16 |
|
note |
1180397 |
11265 |
9.08 |
11.67 |
20.30 |
-8.63 |
|
odd |
242182 |
2663 |
2.15 |
2.76 |
7.20 |
-4.44 |
|
originalsloc |
9959 |
211 |
0.17 |
0.22 |
1.00 |
-0.78 |
|
otherfindaid |
1945 |
247 |
0.20 |
0.26 |
2.30 |
-2.04 |
|
phystech |
8439 |
300 |
0.24 |
0.31 |
1.50 |
-1.19 |
|
prefercite |
1995 |
264 |
0.21 |
0.27 |
0.10 |
0.17 |
|
processinfo |
26332 |
1084 |
0.87 |
1.12 |
3.80 |
-2.68 |
|
relatedmaterial |
16727 |
882 |
0.71 |
0.91 |
4.40 |
-3.49 |
|
runner |
0 |
0 |
0.00 |
0.00 |
0.00 |
0.00 |
|
scopecontent |
1852092 |
33483 |
27.00 |
34.68 |
61.30 |
-26.62 |
|
separatedmaterial |
2784 |
208 |
0.17 |
0.22 |
0.00 |
0.22 |
|
userestrict |
2993 |
580 |
0.47 |
0.60 |
3.20 |
-2.60 |
Table 17: (Wisser Table 20): content tags in dsc, using query //dsc//*.
|
Element |
N |
N_uniq |
% [N_uniq/S] |
% [N_uniq/n=96548] |
% [(N_uniqK)/n=1,053] |
diff |
|
corpname |
373402 |
6082 |
4.90 |
6.30 |
8.40 |
-2.10 |
|
famname |
3644 |
914 |
0.74 |
0.95 |
1.70 |
-0.75 |
|
function |
996 |
53 |
0.04 |
0.05 |
0.00 |
0.05 |
|
genreform |
351956 |
6988 |
5.64 |
7.24 |
5.10 |
2.14 |
|
geogname |
1023771 |
6653 |
5.36 |
6.89 |
6.30 |
0.59 |
|
name |
34339 |
380 |
0.31 |
0.39 |
1.40 |
-1.01 |
|
occupation |
25284 |
285 |
0.23 |
0.30 |
0.40 |
-0.10 |
|
persname |
2610548 |
11970 |
9.65 |
12.40 |
12.90 |
-0.50 |
|
subject |
1239139 |
2419 |
1.95 |
2.51 |
4.70 |
-2.19 |
References
[1] In April 2013, the ArchiveGrid index contained 1,632,246 MARC records, 119,984 EAD records, 61,551 HTML records, and 4,532 PDF records. The EAD count in the index is lower than the set of documents analyzed, to avoid duplicating their display for certain contributors who supply corresponding MARC records.
[2] Library of Congress EAD Website: http://www.loc.gov/ead/index.html; EADiva: http://eadiva.com/.
[3] E-mail to archives and archivists listserv, November 15, 2010.
[4] Wisser, Katherine M, and Jackie Dean, EAD Tag Usage: Community analysis of the use of Encoded Archival Description elements, article submitted for publication in the American Archivist
[5] Smith-Yoshimura, Karen, Catherine Argus, Timothy J. Dickey, Chew Chiat Naun, Lisa Rowlinson de Ortiz, and Hugh Taylor. 2010. Implications of MARC Tag Usage on Library Metadata Practices.
About the Authors
Marc Bron is a researcher at the Intelligent Systems Lab Amsterdam, where he is about to complete his PhD in Information Retrieval. His dissertation focused on improving accessibility to information stored in cultural heritage institutions by developing algorithms and interactive retrieval systems that support exploration and contextualization. During his PhD Marc has published over 20 papers at top tier conferences, journals, and workshops. His current research direction aims to develop new collaborative search methods for users of archival collections.
Bruce Washburn is a Consulting Software Engineer in OCLC Research. He provides software development support for OCLC Research initiatives and participates as a contributing team member on selected research projects. In addition, he provides software development support for selected OCLC Products and Services. At OCLC Washburn has been a part of the product teams that developed and maintain CAMIO, ArchiveGrid, the WorldCat Search API, and OAIster.
Merrilee Proffitt is a Senior Program Officer in OCLC Research. She provides project management skills and expert support to institutions represented within the OCLC Research Library Partnership. Merrilee has authored or co-authored articles, guidelines, and reports for a variety organizations and professional journals. She is frequently an invited speaker at international professional conferences and workshops on topics relating to digital libraries and special collections. Her current projects and interests include: archival description, increasing access to special collections, looking at developing better relationships between Wikipedia and cultural heritage institutions, and how Massively Open Online Courseware (MOOCs) may impact libraries. She is a member of the small but mighty ArchiveGrid team.


Subscribe to comments: For this article | For all articles
Leave a Reply